Note 3 - 03/03/2023
TABLE OF CONTENTS
I. Introduction to polar coordinate
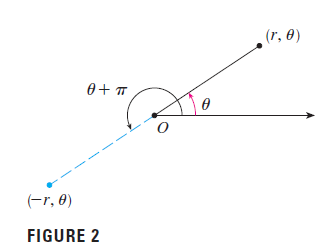
We choose a point in the plane that is called the pole (or origin) and is labeled $O$. Then we draw a ray (half-line) starting at $O$ called the polar axis. This axis is usually drawn horizontally to the right and corresponds to the positive $x$-axis in Cartesian coordinates.
If is any other point in the plane, let $r$ be the distance from $O$ to $P$ and let $\theta$ be the angle $\theta$ (usually measured in radians) between the polar axis and the line $OP$ as in Figure 1. Then the point is represented by the ordered pair $(r,\theta)$ and $r$, $\theta$ are called polar coordinates of $P$. We use the convention that an angle is positive if measured in the counterclockwise direction from the polar axis and negative in the clockwise direction.

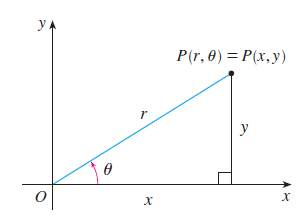
The connection between polar and Cartesian coordinate can be seen from below:
II. Polar curves
The graph of a polar equation $r=f(\theta)$, consists of all points $P$ that have at least one polar representation $(r,\theta)$ whose coordinates satisfy the equation.
Example:
- Sketch the curve with polar equation $r=2 \cos\theta$

We can derive polar equation to $x,y$ equation as follows:
\[\begin{align*} &r=2\cos\theta \\ \Leftrightarrow \ &r^2 = 2r\cos\theta \\ \Leftrightarrow \ &x^2+y^2 = 2x \\ \Leftrightarrow \ &(x-1)^2+y^2=1 \end{align*}\]We can see that the above equation describing the circle exactly as in the graph.
- Sketch the curve $r=1+\sin\theta$
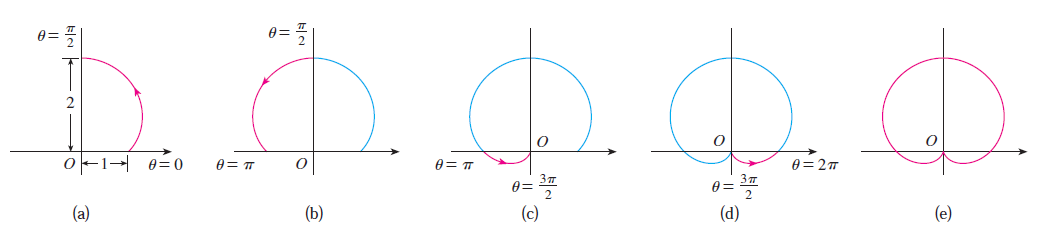
Last update: 18:34 - 07/03/2023