Note 4 - 06/03/2023
TABLE OF CONTENTS
I. Areas and lengths in polar coordinates
1. Area
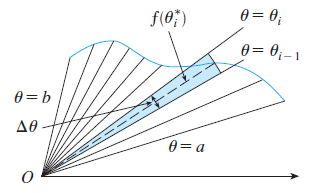
The formula for the area $A$ of the polar region is:
\[A=\int_a^b \frac{1}{2} [f(\theta)]^2 d\theta=\int_a^b \frac{1}{2} r^2 d\theta\]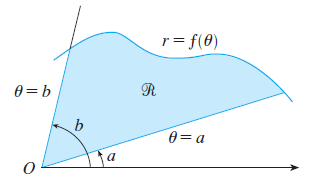
2. Arc length
The length $L$ of a curve with polar equation $r=f(\theta)$, $a \leq \theta \leq b$, is:
\[L=\int_a^b \sqrt{r^2+\left(\frac{dr}{d\theta}\right)^2} \ d\theta\]We can obtain the above formula by using the fomula calculating the arc length of parametric curve and Product Rule:
\[x=r\cos\theta \ \ \ \ \ \ y=r\sin\theta\] \[\frac{dx}{d\theta}=\frac{dr}{d\theta}\cos\theta-r\sin\theta \ \ \ \ \ \ \ \ \frac{dy}{d\theta}=\frac{dr}{d\theta}\sin\theta+r\cos\theta\]So, using \(\sin^2\theta+\cos^2\theta=1\), we have:
\[\begin{align*} &\left(\frac{dx}{d\theta}\right)^2+\left(\frac{dy}{d\theta}\right)^2 \\ =&\left(\frac{dr}{d\theta}\cos\theta-r\sin\theta\right)^2+\left(\frac{dr}{d\theta}\sin\theta+r\cos\theta\right)^2 \\ =&\left(\frac{dr}{d\theta}\cos\theta\right)^2 + (r\sin\theta)^2 + \left(\frac{dr}{d\theta}\sin\theta\right)^2 + (r\cos\theta)^2 \\ =& \ r^2+\left(\frac{dr}{d\theta}\right)^2 \end{align*}\] \[\therefore L=\int_a^b \sqrt{\left(\frac{dx}{d\theta}\right)^2+\left(\frac{dy}{d\theta}\right)^2} \ d\theta=\int_a^b \sqrt{r^2+\left(\frac{dr}{d\theta}\right)^2} \ d\theta\]Last update: 18:34 - 07/03/2023