Physics II - B10

Proofread by Huỳnh Hà Phương Linh

Electromotive force (Suất điện động)
Internal Battery Resistance
Load Resistance
Combination of resistors
- In Series:
- In parallel:
Kirchhoff’s Rules
RC Circuit
Other references

Electromotive force (Suất điện động)

\[\xi = emf \,\ (volt)\]

Internal Battery Resistance

\[\Delta V = \xi - I.r\] \[I = \frac{\xi}{R+r}\] \[\Delta V = R.\frac{\xi}{R+r}\] \[P = I.\xi = I^2.(R+r)\]

Load Resistance

Combination of resistors

In Series:

\[I_1 = I_2 = I\] \[\Delta V = \Delta V_1 + \Delta V_2\] \[R = R_1 + R_2\]

In parallel:

\[\Delta V_1 = \Delta V_2 = \Delta V\] \[I = I_1 + I_2\] \[\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}\]

Kirchhoff’s Rules

Juntion rule: $\sum I_{in} = \sum I_{out}$
Loop rule: $\sum \Delta V = 0$

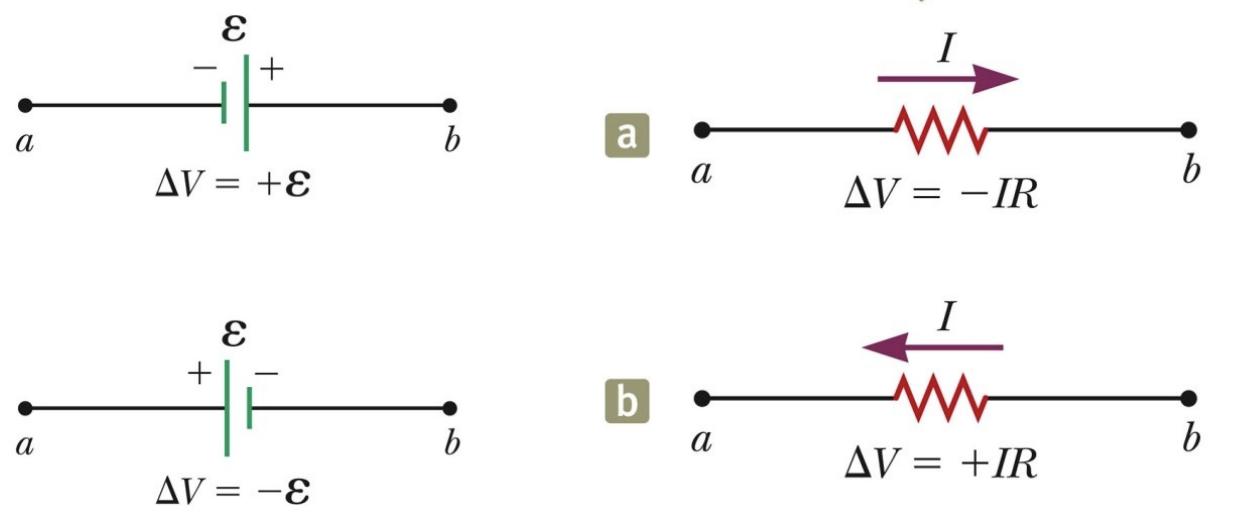
RC Circuit

Loop Rule:

\[\xi - \frac{Q}{C} - R.i = 0\] \[\xi - \frac{Q}{C} - R.\frac{dQ}{dt} = 0\] \[\xi - \frac{Q}{C} = R\frac{dQ}{dt}\] \[\xi C - Q = RC\frac{dQ}{dt}\] \[\displaystyle \int_0^t \frac{-dt}{RC} = \int_0^q \frac{dQ}{Q - \xi C}\] \[\ln(\frac{q-C\xi}{-C\xi}) = -\frac{t}{RC}\]

Notes:
$q(t) = \xi.C(1-e^{\frac{-t}{RC}}) = Q_{max}.(1-e^{\frac{-t}{RC}})$
$i(t) = \frac{dQ}{dt} = \frac{\xi}{R}.e^{\frac{-t}{RC}}$
$\tau = RC (s):$ time constant