Physics II - B11

\[P = I^2R\] \[\displaystyle P = \frac{\Delta V^2}{(R+r)^2}R = \Delta V^2\frac{1}{(\sqrt{R} +\frac{r}{\sqrt{R}})^2} \leqslant \frac{\Delta V^2}{4r}\]

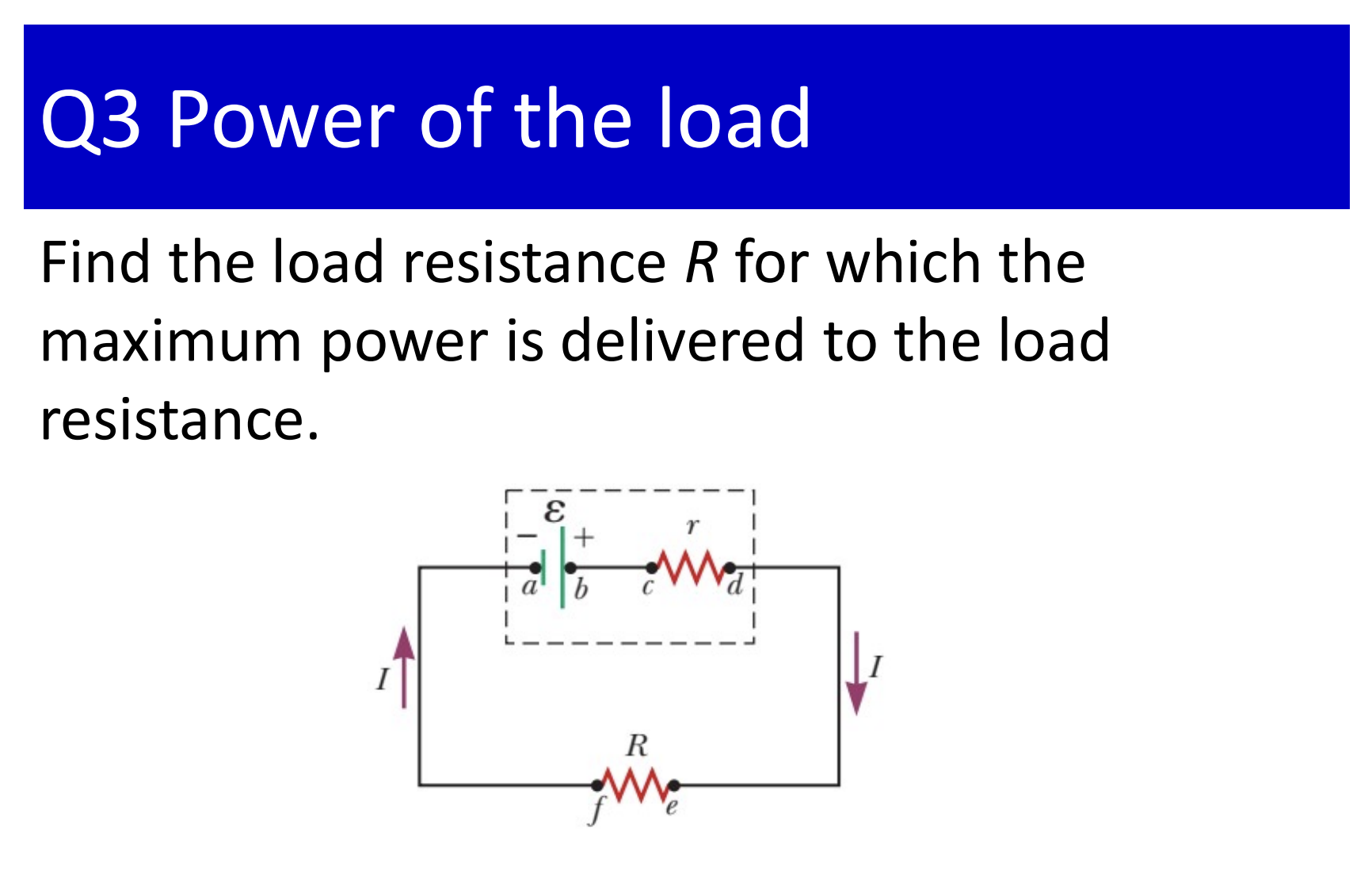
• The $”=”$ exists when $R = r$.

\[a)\,\ \displaystyle I = \frac{\xi}{R+r} = \frac{12.6}{5 + 0.08} = 2.48 (A)\] \[\Delta V = IR = 2.48 \times 5 = 12.4 (V)\]

$b)$ Let $I_1$ be the current flowing through the automobile battery, $I_2$ be the current flowing through the headlight bulbs. From the Kirchhoff’s law, we get:

\[I_1 = I_2 + 35A\] \[\displaystyle \xi = I_1r + I_2R = (I_2 + 35)r + I_2R\] \[\displaystyle I_2 = \frac{\xi - 35r}{R+r} = 1.93(A)\] \[\Delta V = I_2R = 1.93 \times 5 = 9.65(V)\]

• When $S$ is open $:$

\[\displaystyle I_1 = 10^{-3} = \frac{6}{R_1+R_2+R_3} (1)\]

• When $S$ is closed at position $a:$

\[\displaystyle I_2 = 1.2 \times 10^{-3} = \frac{6}{R_1 + \frac{R_2}{2} + R_3} (2)\]

• When $S$ is closed at position $b:$

\[\displaystyle I_3 = 2 \times 10^{-3} = \frac{6}{R_1 + R_2} (3)\]

• From $(1)(2)(3)$ $\to R_1 =$ $1$ $k \Omega,$ $R_2 = 2$ $k \Omega,$ $R_3 = 3$ $k \Omega.$

• The potential difference from $a$ to $b$ following path $I_1:$

\[V_b - V_a = 24 -I_1\times 6\Omega = 6(V)\]

• The potential difference from $a$ to $b$ following path $I_2:$

\[V_b - V_a = -3I_2 (V)\]

• Therefore $:$

\[-3I_2 = 6 \to I_2 = -2(A)\]

$b)$ $I_3 =I_1 + I_2 = 3-2 = 1(A)$

$c)$ Nooo…Because we don’t have enough equations to calculate both $\xi$ and $R.$

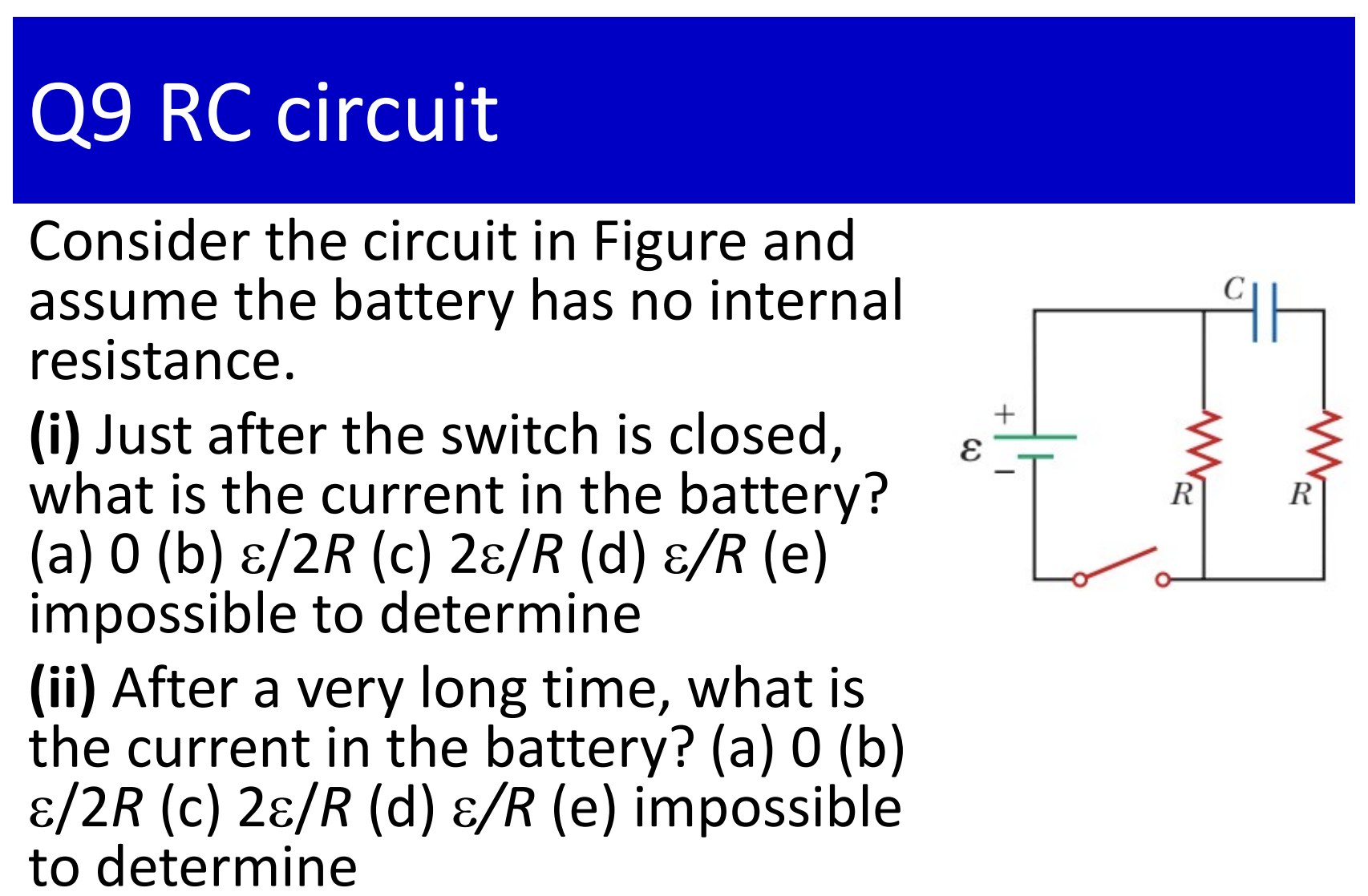
$i)$ $C$
$ii)$ $D$

$a)$ $\tau = RC = (R_1 +R_2)C = 1.5 (sec)$

$b)$ $\tau = R_2C = 0.5(sec)$

$c)$ $\displaystyle I_1 = \frac{\xi}{R_1}$, $\displaystyle I_2 = \frac{\xi}{R_2}e^{\frac{-t}{R_2C}}$

The total current in the switch is $:$ $\displaystyle I = \xi\bigg[\frac{1}{R_1}+\frac{e^{\frac{-t}{R_2C}}}{R_2} \bigg]$

---