Physics II - B18
TABLE OF CONTENTS
- The RLC Circuit
- The LC Circuit
- Damped Oscillators (Dao động tắt dần)
- AC Circuit
- Inductors in an AC Circuit
- Capacitors in an AC Circuit
- RC circuit
- RLC circuit
The RLC Circuit

We have $:$
\[\Delta U_E + \Delta U_B + \Delta E_{int} = 0\]Now differentiate this equation with respect to time $:$
\[\frac{dU_E}{dt} + \frac{dU_B}{dt} + \frac{dE_{int}}{dt} = 0\]We have two equations $:$
\[\Delta U_E = \frac{q^2}{2C}\] \[\Delta U_B = \frac{1}{2}Li^2\]Recognizing that the third derivative is the rate at which energy is delivered to the resistor $:$
\[\frac{q}{C}\frac{dq}{dt} + Li\frac{di}{dt} + i^2R = 0\]And $:$
\[i = \frac{dq}{dt}\]So $:$
\[L\frac{d^2q}{dt^2} + R\frac{dq}{dt} + \frac{q}{C} = 0\] \[q'' + \frac{R}{L} q' + \frac{1}{LC} = 0\]Let $:$ $q(t) = e^{mt}$
\[m^2 + 2\frac{R}{2L}m + \frac{1}{LC} = 0\] \[\Delta' = (\frac{R}{2L})^2 - \frac{1}{LC}\]$\Delta > 0 :$
\[m = -\frac{R}{2L} \pm \sqrt{(\frac{R}{2L})^2 - \frac{1}{LC}}\] \[q(t) = C_1e^{m_1t} + C_2e^{m_2t}\]$\Delta = 0:$
\[m = -\frac{R}{2L}\] \[q(t) = e^{mt}(At+B)\]$\Delta < 0:$
\[m = -\frac{R}{2L} \pm i\sqrt{(\frac{R}{2L})^2 - \frac{1}{LC}}\] \[q(t) = C_1e^{m_1t} + C_2e^{m_2t}\]The LC Circuit

We have :
\[\Delta U_E + \Delta U_B = 0\]Now differentiate this equation with respect to time $:$
\[\frac{d}{dt} \bigg(\frac{q^2}{2C} + \frac{1}{2}Li^2\bigg) = \frac{q}{C}\frac{dq}{dt} + Li\frac{di}{dt}=0\] \[\frac{d^2q}{dt^2} +\frac{q}{LC} = 0 \to q''(t) + \frac{1}{LC}q(t) = 0\]So :
\[q(t) = Q_0cos(\omega t + \varphi)\] \[i(t) = \omega Q_0sin(\omega t + \varphi)\]Damped Oscillators (Dao động tắt dần)

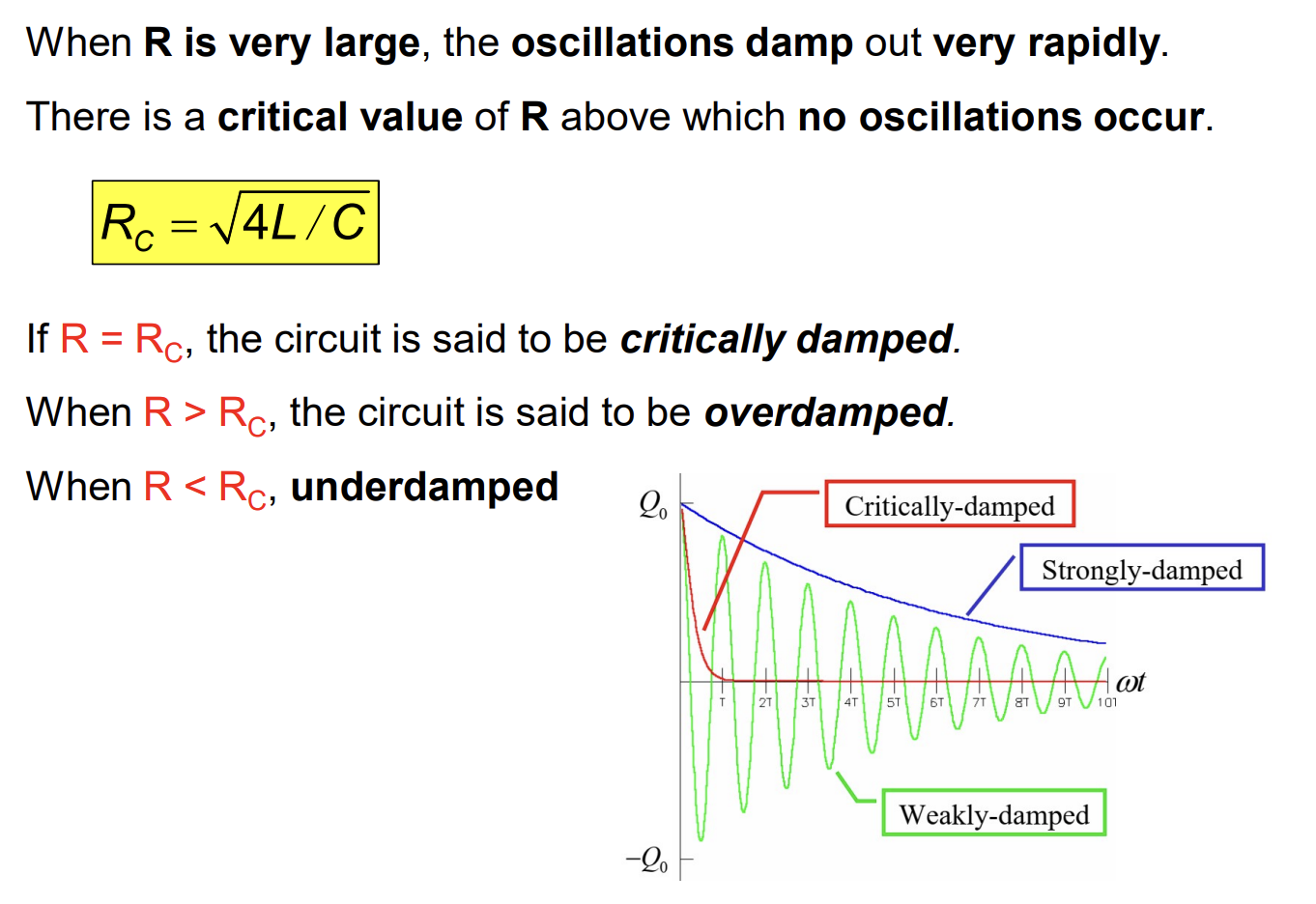
AC Circuit
Resistors in an AC Circuit
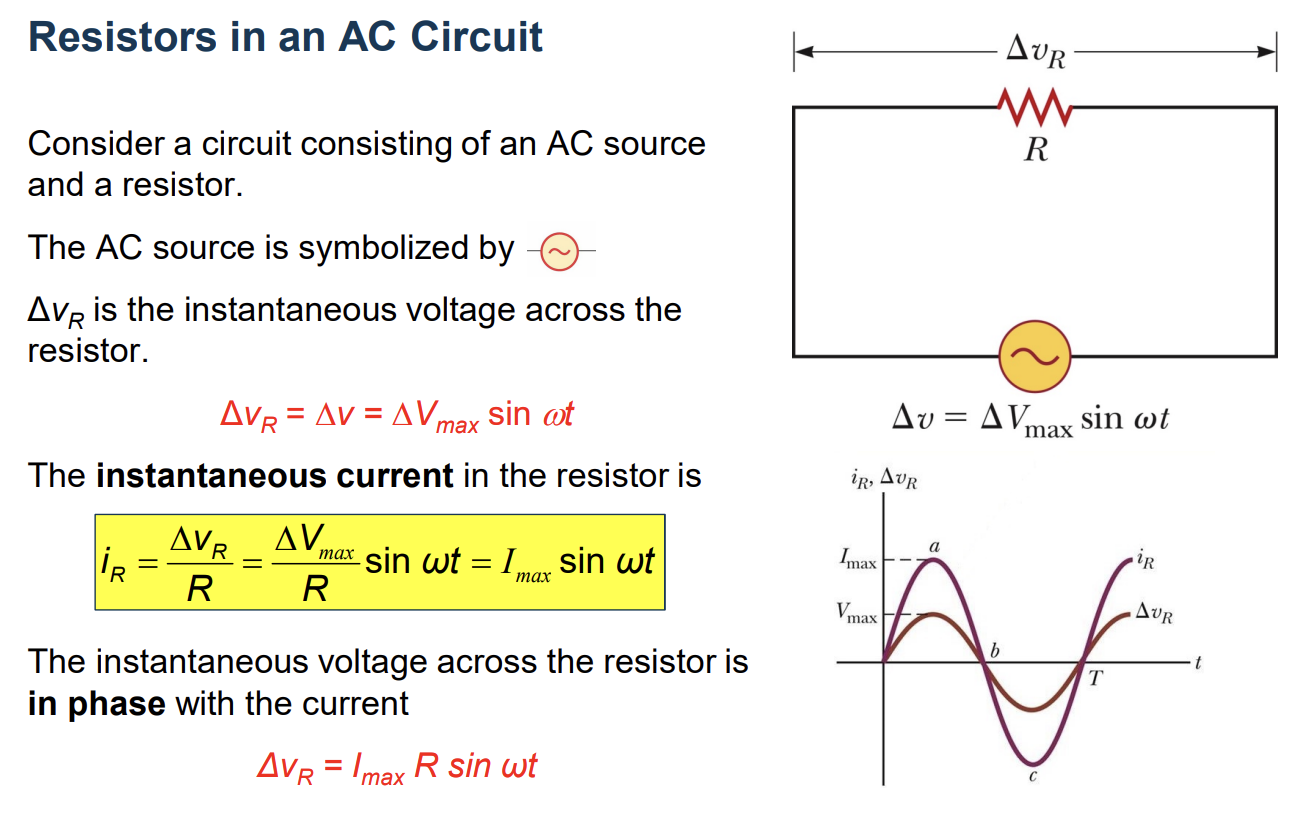
rms Current and Voltage
\[\Delta V_{rms} = \frac{\Delta V_{max}}{\sqrt{2}}\] \[\Delta I_{rms} = \frac{\Delta I_{max}}{\sqrt{2}}\]Power
\[P = i^2R = i_R \Delta v = \Delta V_{max}I_{max}sin^2(\omega t)\] \[P_{avg} = I^2_{rms}R\]Inductors in an AC Circuit
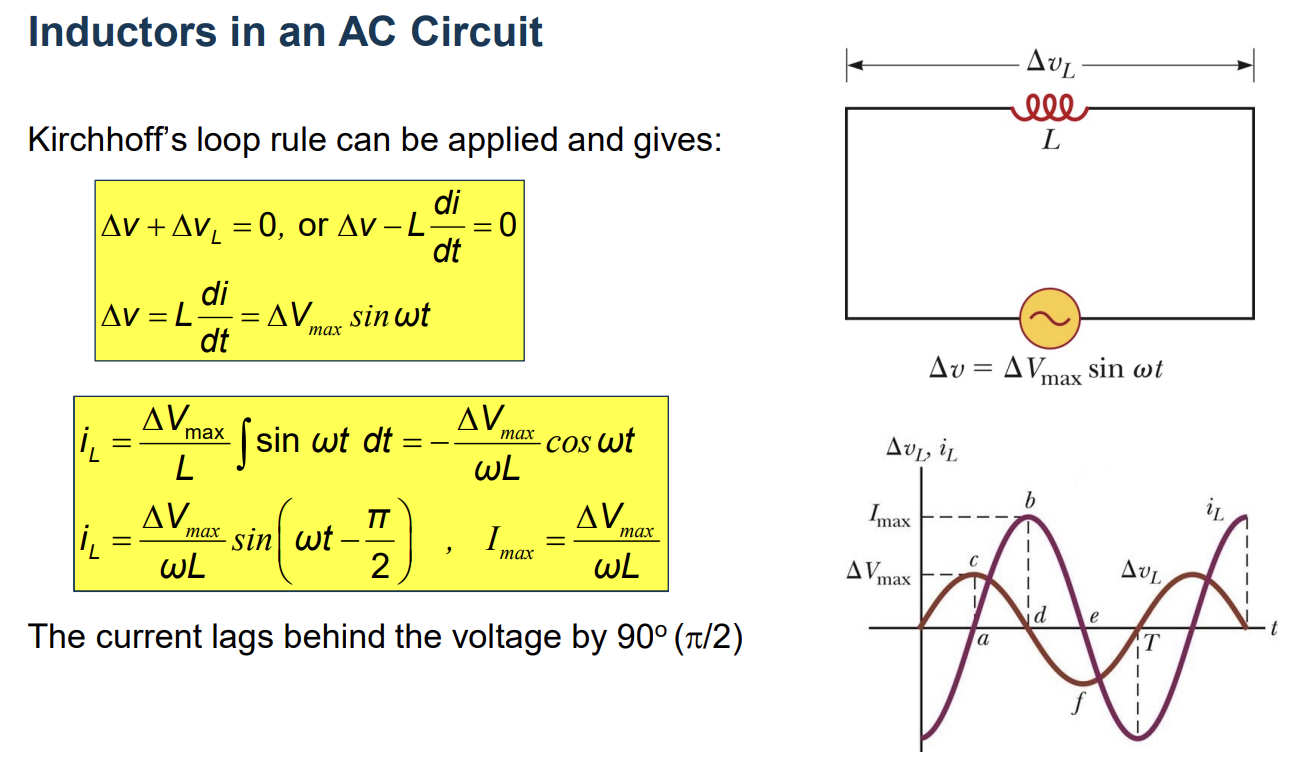
Capacitors in an AC Circuit
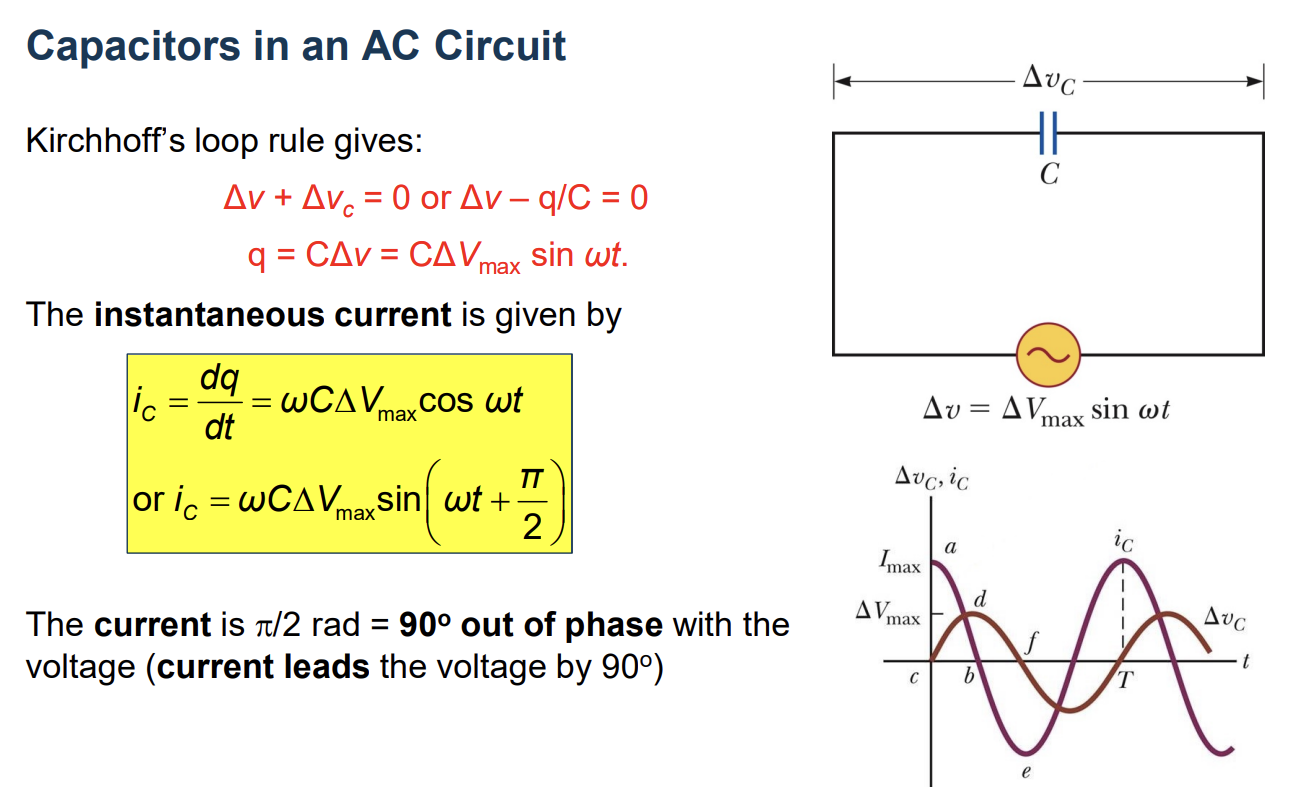
RC circuit
\[I_{max} = \frac{\Delta V_{max, R}}{R} = \frac{\Delta V_{max, C}}{Z_C}\] \[\Delta V_{max} = \sqrt{\Delta V_{max, R}^2 + \Delta V_{max, C}^2} = I_{max}\sqrt{R^2 + Z_C^2}\]RLC circuit
