Physics II - B19
TABLE OF CONTENTS
Chapter 33
Difference between E & M

Maxwell’s Equations

Lorentz Force Law

Electromagnetic Waves in Free Space
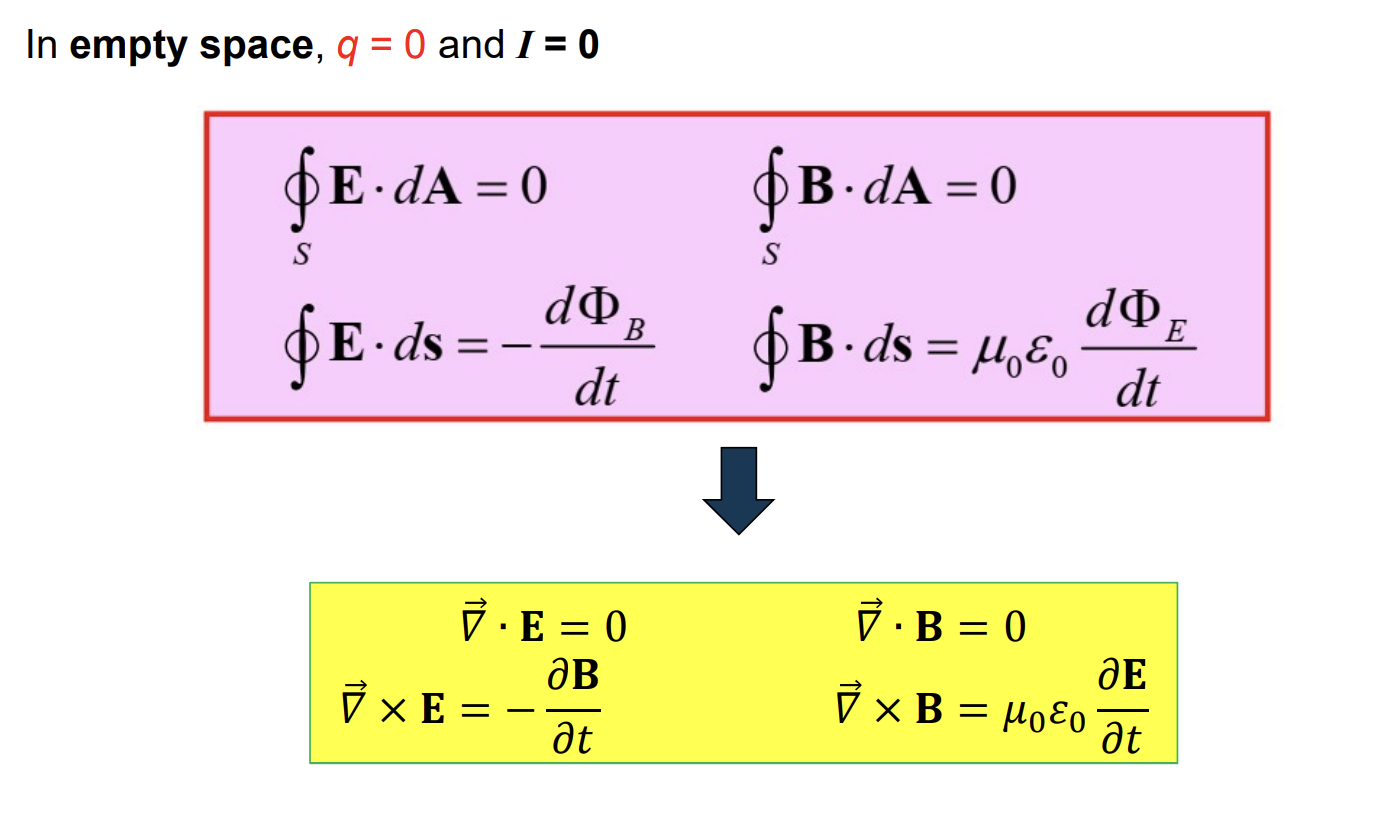
Plane Electromagnetic Waves
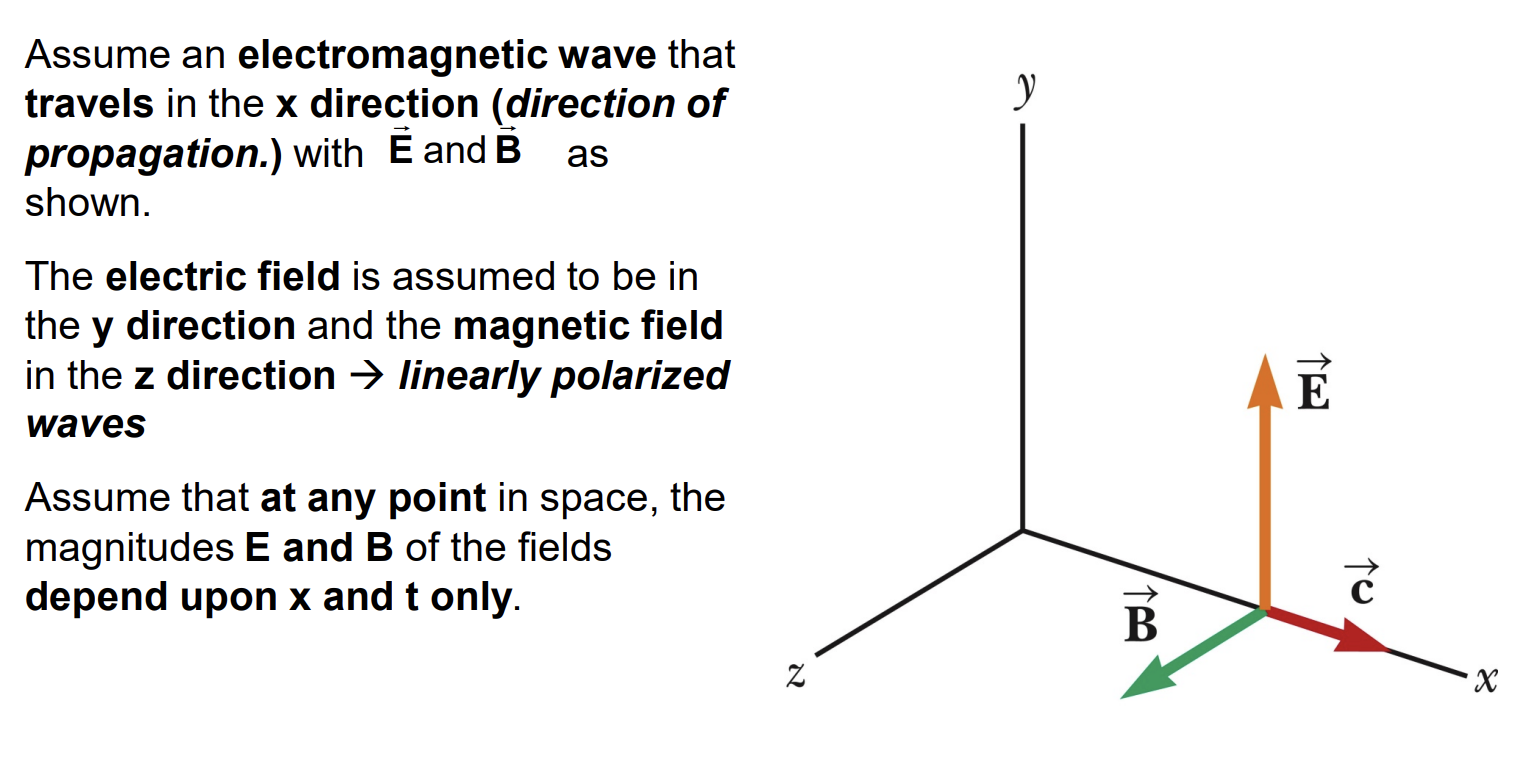
E to B Ratio

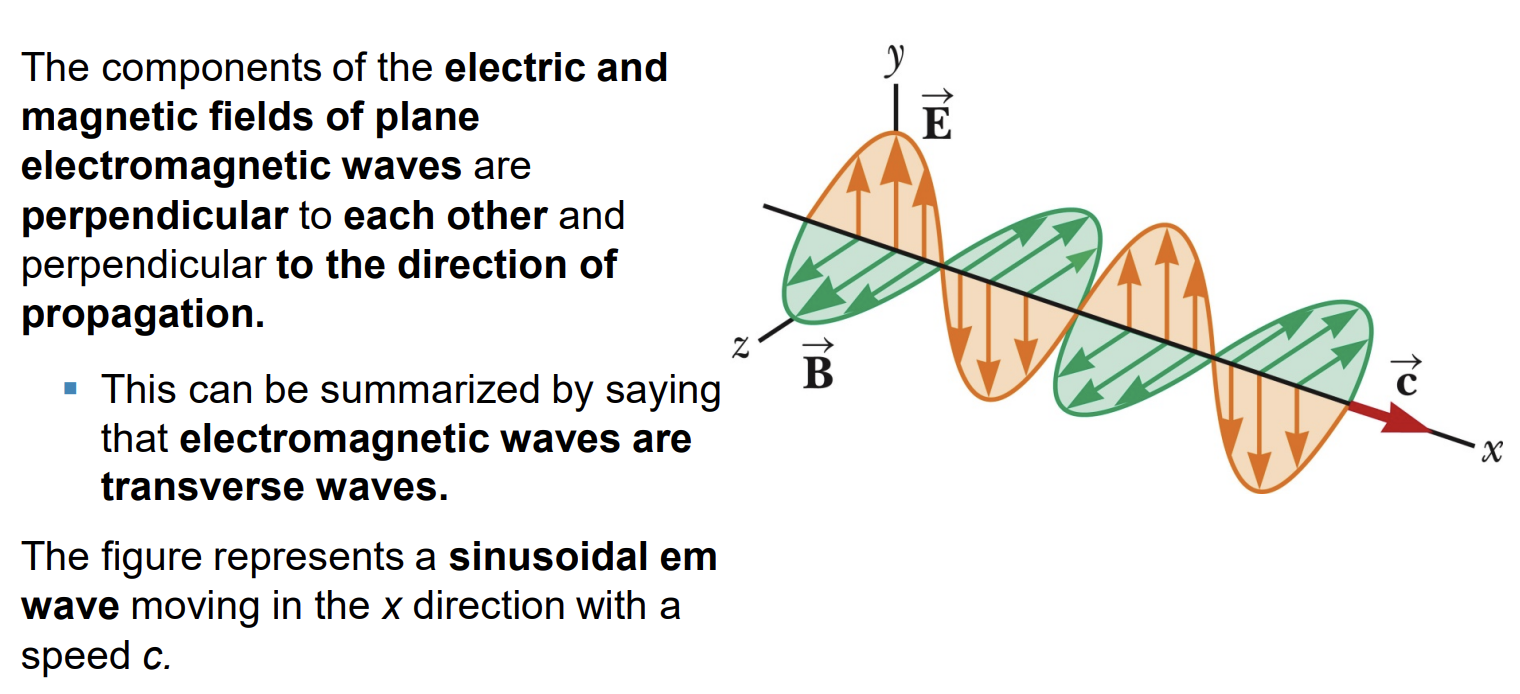
Properties of EM Waves
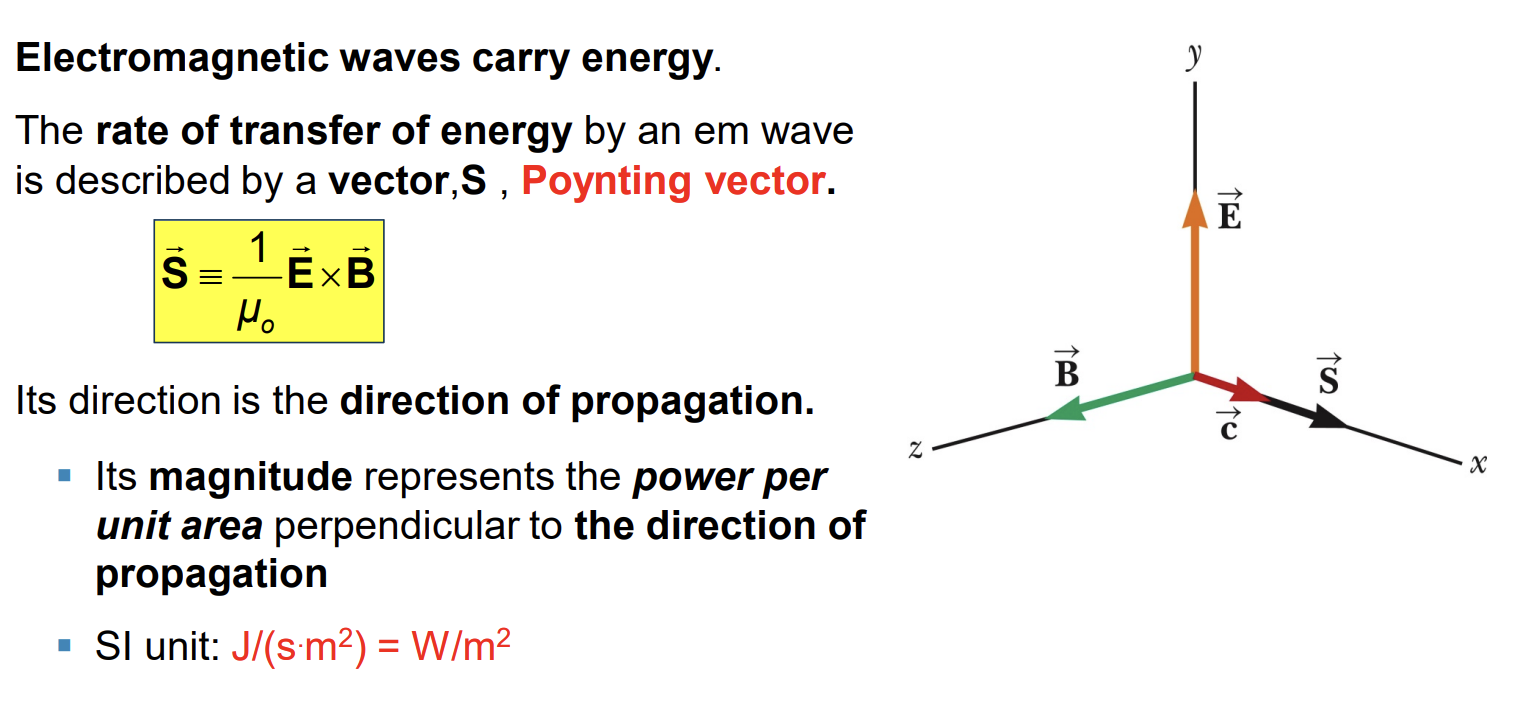
Poynting Vector
Intensity

Energy Density
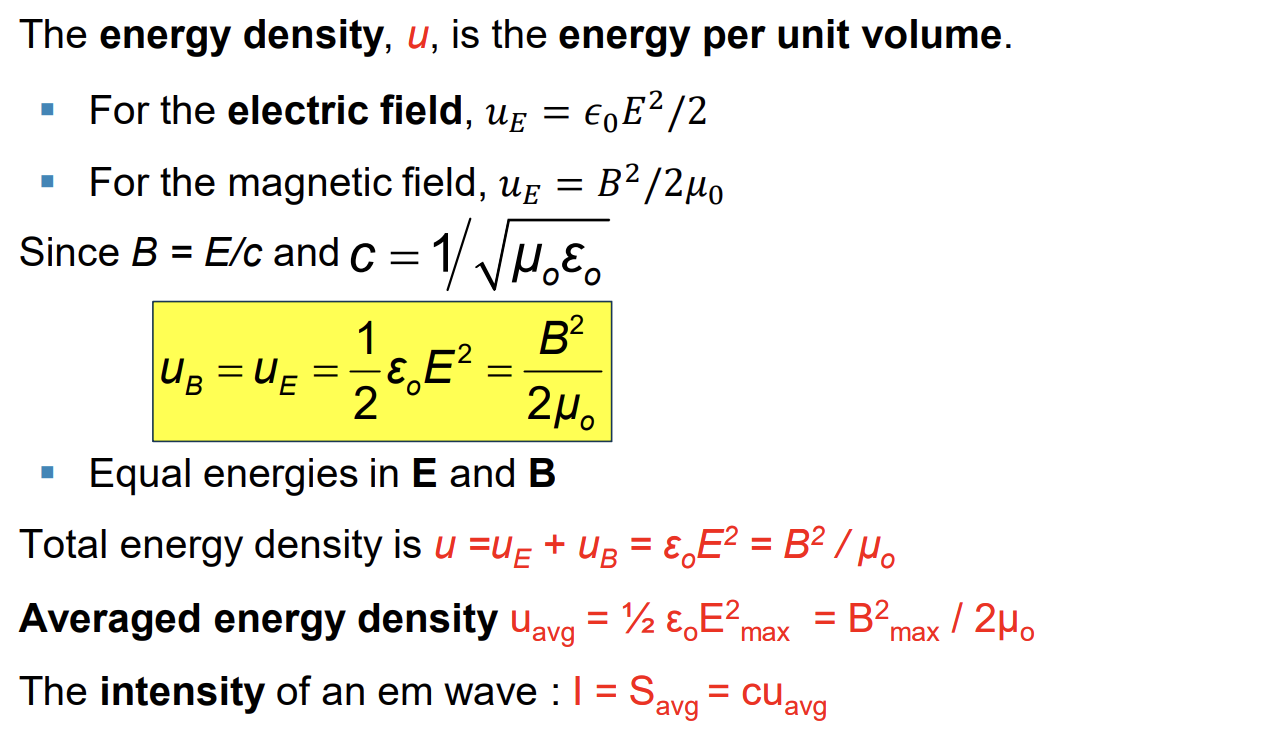
Assignments Chap 31

$i)$ When $S_1$ is closed $(t = 0):$
\[i = 0\] \[\Delta V_R = Ri = 0\] \[\Delta V_L = L\frac{di}{dt} = \xi\]$ii)$ After a very long time $:$
\[i = \frac{\xi}{R}\] \[\Delta V_R = Ri = \xi\] \[\Delta V_L = L\frac{di}{dt} = 0\]
The magnetic flux through each turn $:$
\[L = \frac{N\Phi_B}{i} \to \Phi_B = \frac{LI}{N} = 19.2 \mu (Wb)\]
$S$ is closed for a long time $:$
\[I = \frac{\xi}{R} = 0.2(A)\]After $S$ is opened, we have an $LC$ circuit, by conservation of energy $:$
\[LI^2 = CU^2 \to L = 0.281(H)\]Assignments Chap 32

The current $:$
\[i_L = I_{max}sin(\omega t + \varphi)\] \[u_B = \frac{1}{2}Li^2 = \frac{1}{2}L\frac{2(\Delta V_{rms})^2}{(\omega L)^2}sin(\omega t + \varphi)^2\]At $t = 0(s):$
\[u_B = 0 \to sin(\varphi)^2 = 0 \to \varphi = 0\]At $t = \frac{1}{180}(s):$
\[u_B = \frac{1}{2}Li^2 = \frac{1}{2}L\frac{2(\Delta V_{rms})^2}{(\omega L)^2}sin(\omega t)^2 = 3.8(J)\]
$a)$
\[\displaystyle \frac{\Delta V_{out}}{\Delta V_{in}} = \frac{IR}{IZ} = \frac{R}{\sqrt{R^2 + \frac{1}{(\omega C)^2}}}\]$b)$ When the frequency decreases toward zero, the ratio will go to $0.$
$c)$ When the frequency increases without limit, the ratios will go $1.$

$a)$
\[f_{res} = \frac{1}{2\pi}\sqrt{\frac{1}{LC}} = 3.56 \times 10^3 (Hz)\]$b)$
\[I_{max} = \frac{\Delta V_{max}}{R} = 5(A)\]$c)$
\[\Delta V_L = Z_L I_{max} = 2.24 \times 10^3 (V)\]