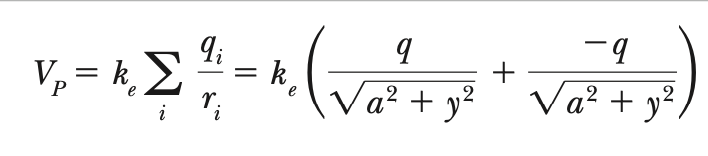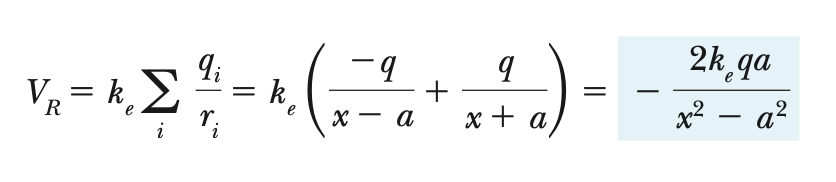Physics II - B05
TABLE OF CONTENTS
- Work (Work done by the field)
- Work - KE theorem of a particle
- Charged Particle in a Uniform Field
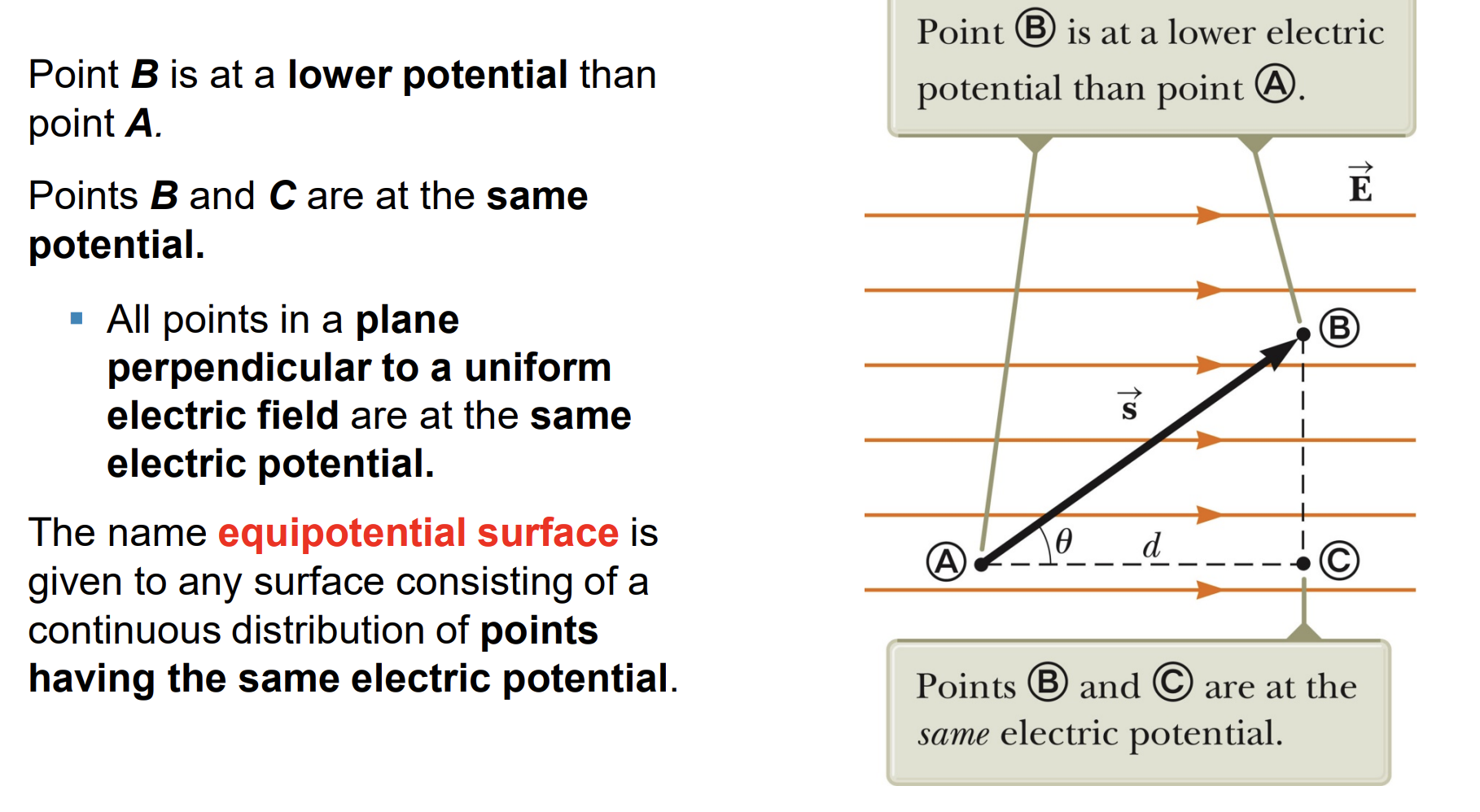
- Equipotential Surface (Mặt đẳng thế)
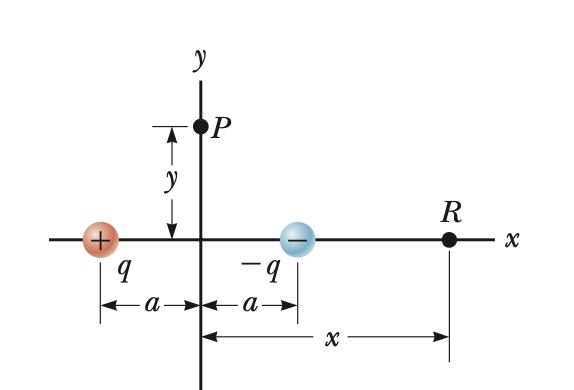
- Potential and Point Charges
- Notes
- System of charges
- Assignments
- Other references
Work (Work done by the field)
\[\displaystyle W_{field} = \int \vec F. d\vec s = \int F.ds.cos\theta = \int_{line} q.\vec E. d\vec s\]Work - KE theorem of a particle
\[W_{field} = \Delta K = K_f -K_i\]System = a charge + the field : isolated
\[\Delta K - W_{field} = 0 \, (W_{field} = \Delta U)\] \[\Delta K + \Delta U = 0 \to \Delta E = 0\] \[\displaystyle \Delta U = - \int_{initial}^{final} q.\vec E. d\vec s = U_f - U_i = q.\Delta V\] \[\to \Delta V = \frac{\Delta U}{q} = V_f - V_i\]Therefore: \(\displaystyle Choose \, V_i = 0 \to V_f = -\int_i^f \vec E.d \vec s\)
[energy] = 1eV = $1,6.10^{-19} (J)$ [electric field] = $\frac{V}{m}$ = $\frac{N}{C}$
Charged Particle in a Uniform Field

Equipotential Surface (Mặt đẳng thế)
Potential and Point Charges
.png)
Notes
- Vecto $\bot$ với mặt cong $\Leftrightarrow$ Vecto $\bot$ tiếp tuyến của mặt cong tại điểm đó.
- Orthonomal: trực chuẩn
- Potential energy of the system:
- Charge
- Field
System of charges
\(\displaystyle \Delta V = -\int E_{net}.d \vec s = - \int(\sum \vec E).d \vec s\)
\[\displaystyle = -\sum \int\vec E.d\vec s = \sum \Delta V\]Choose $V_{\infty} = 0:$ \(V = \sum\frac{k.Q_i}{r_i}\)
Assignments