Skip to main content Link Menu Expand (external link) Document Search Copy Copied

Physics II - B06

TABLE OF CONTENTS

Finding E from V

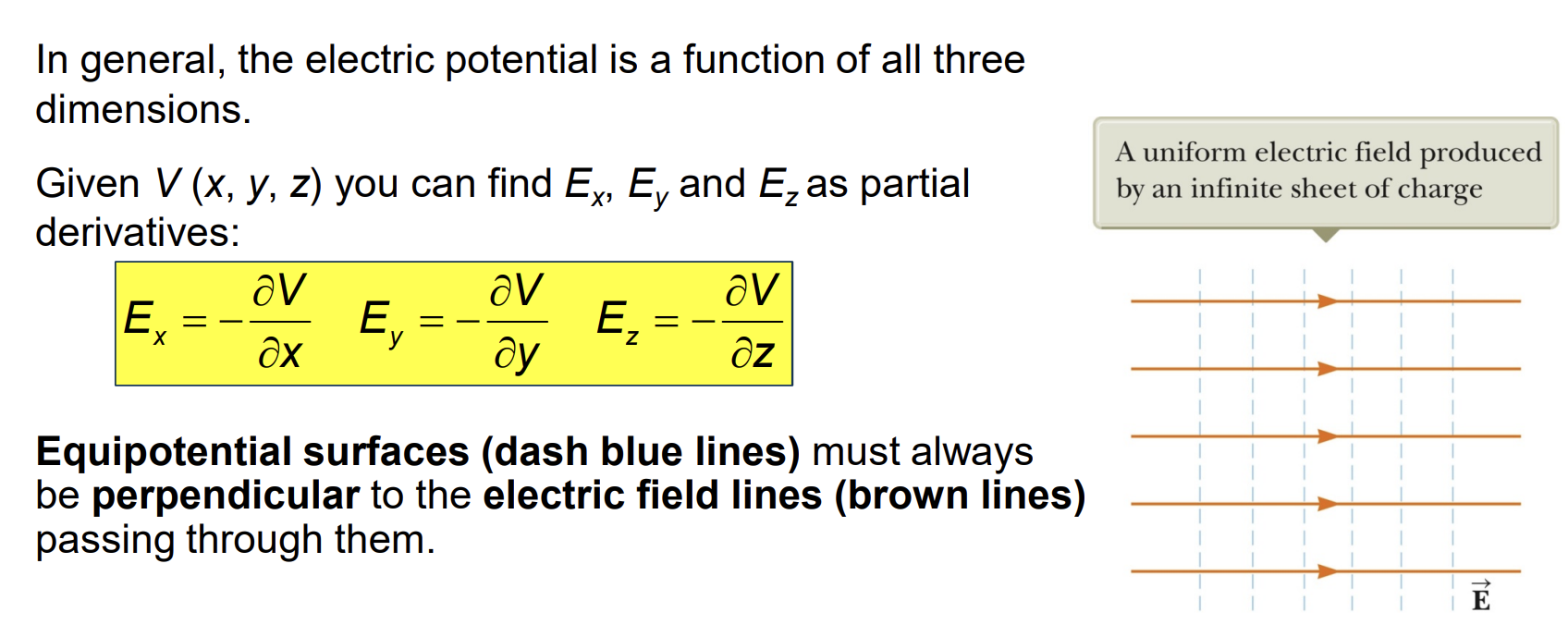
Assignments

Problem 1

\[E = \frac{\lambda}{2.\pi.\epsilon_0.r}\] \[\displaystyle \Delta V = -\int_A^B \vec E.d\vec s = -\int_C^B \vec E.d\vec s = -\int_C^B E.dr\] \[\displaystyle = -\int_{r_{a}}^{r_b} \frac{\lambda}{2\pi.\epsilon_0.r}.dr\] \[Choose \,\ r_a \,\ where \,\ V_A = 0:\] \[V(r) = -\frac{\lambda}{2\pi\epsilon_0}.\ln r +const\]

Problem 2

Problem 3

\[r \geqslant R: E(r) = \frac{1}{4\pi\epsilon_0}.\frac{Q}{r^2}\] \[r < R: E(r) = \frac{1}{4\pi\epsilon_0}.\frac{Q.r}{R^3}\]

$r \geqslant R:$

\[\displaystyle \Delta V = -\int_A^B \vec E.d \vec s = -\int_A^B E.dr\] \[= -\frac{Q}{4\pi.\epsilon_0}.\bigg(\frac{1}{r_a} - \frac{1}{r_b}\bigg)\] \[V_{\infty} = 0 \to V(r) = \frac{1}{4\pi \epsilon_0}.\frac{Q}{r}\]

Conductor in electrostatic equilibrium

  • $\vec E_{inside} = 0$
  • $V_{inside} = const$
  • $\Delta V= 0$ between any two points on the surface.
  • Extra charges on the surface. Notes: $\vec E$ is vertical because if not, it will create an angle so it will have the tangent component so it will move which is illogical with “electrostatic” (No moving charges) $\to \vec E \bot$ surface

Irregularly Shaped Objects

  • Nguyên lý hoạt động của cột ngư lôi
  • Vì vật nhọn thì $\sigma$ sẽ lớn $\to E$ lớn $\to q$ lớn $\to$ dễ tích điện.

Notes:

  • Solid sphere $\to$ insulating.
  • If conductor $\to$ charges on surface.

Other references